

The column labeled Cumulative Frequency in Table 1.6 is the cumulative frequency distribution, which gives the frequency of observed values less than or equal to the upper limit of that class interval. Handling ordinal, interval, and ratio scale measurements can be a little more complicated, but, as subsequent discussion will show, we can easily handle such data simply by correctly defining the classes. For example, the variable exter has three values, Brick, Frame, and Other. Nominally scaled variables naturally have these classes or categories. Because we count each observation only once, if we add up the number (called the frequency) of houses in all the classes, we get the total number of houses in the data set.

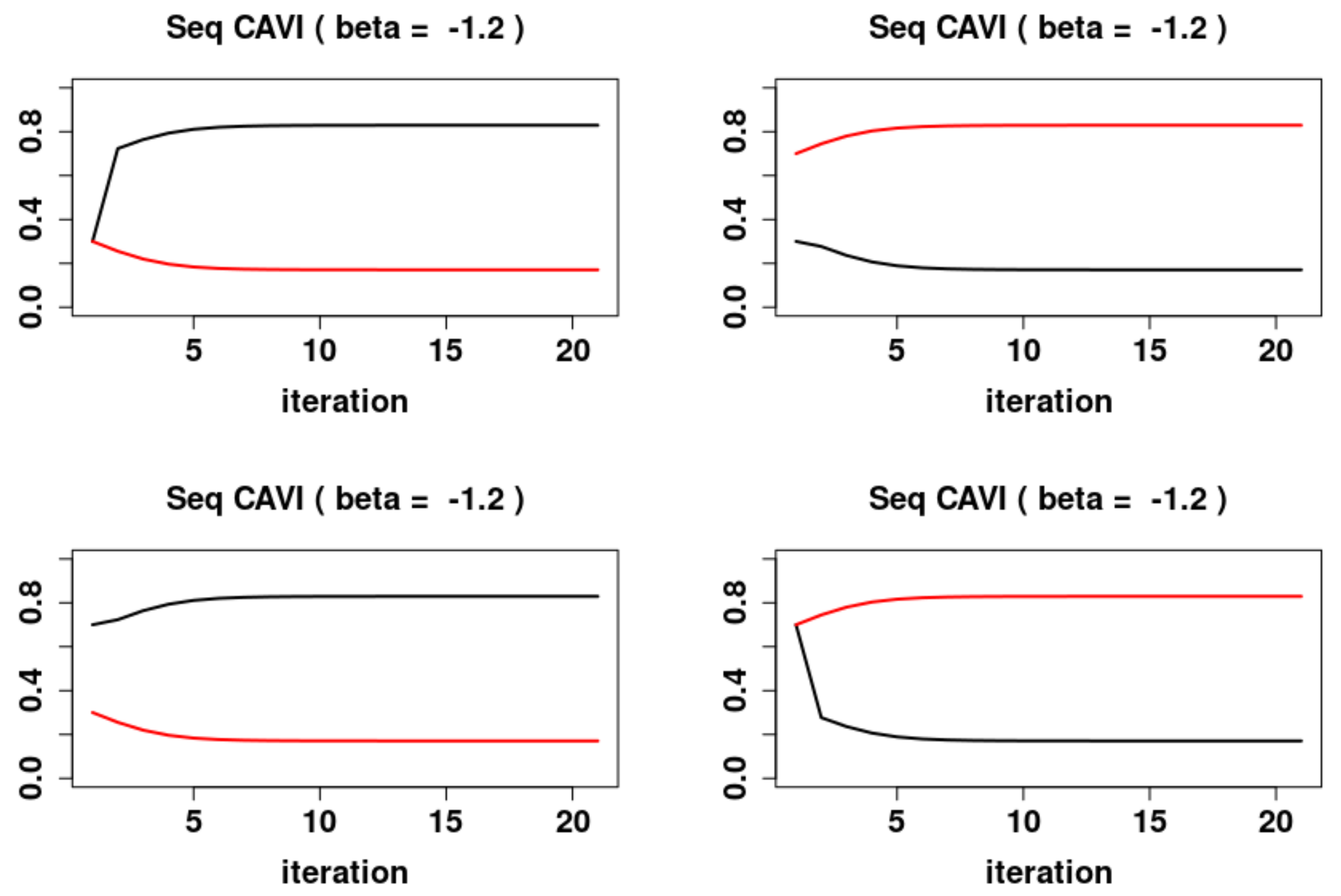
Because we want to count each house only once, these categories (called classes) are constructed so they don’t overlap. To provide more information, we will construct frequency distributions by grouping the data into categories and counting the number of observations that fall into each one. We might be able to conclude that most of the houses have brick exteriors, or that the selling price of houses ranges from $30,000 to $395,000, but a lot more information about this data set can be obtained through the use of some rather simple organizational tools. Very little information about the characteristics of recently sold houses can be acquired by casually looking through Table 1.2. Freund, in Statistical Methods (Fourth Edition), 2022 1.4 Distributions (This provides the information in a table half as long.) From Table 6.1, 1.75 σ yields an area halfway between 0.045 and 0.036, or about 4% of tumors are less than 1 cm.ĭonna L. Since the normal curve is symmetric, the area under the curve to the left of μ−1.75 σ is the same as the area to the right of μ+1.75 σ. About 1.4% of tumors are larger than 5 cm.Īs further illustration, what percent of tumors are less than 1 cm? 1 cm lies 2.77−1=1.77 cm or 1.77/1.01=1. Table 6.1 shows the area in the right tail to the right of 2.20 is 0.014. The value 5 cm lies 5−2.77=2.23 cm to the right of μ.
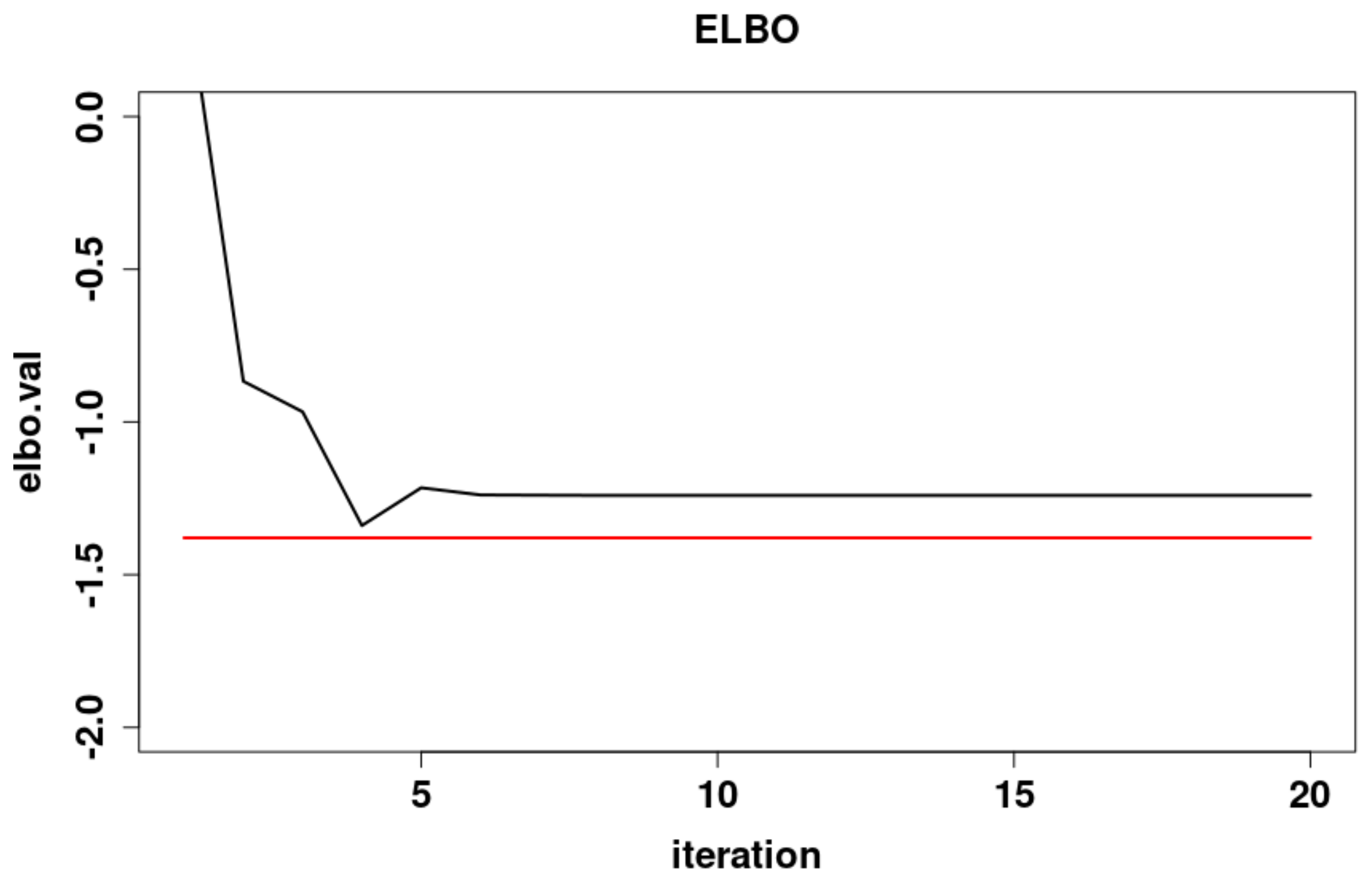
If we are willing to accept the normal curve as the probability distribution of liver tumor sizes, the probability of a tumor larger than 5 cm is the proportion of curve greater than 5. We ask what percent of tumors are larger than 5 cm. Let us denote mean by μ and standard deviation by σ for shorthand. A normal curve with the same mean (2.77 cm) and standard deviation (1.01 cm) is superposed. Riffenburgh, in Statistics in Medicine (Third Edition), 2012 Probability of Certain Ranges Occurringįigure 3.4 shows the relative frequency distribution of tumor sizes of 115 liver cancers. Professor Fligner is currently associated with the Center for Statistical Analysis in the Social Sciences at the University of California at Santa Cruz.R.H. He has been an Associate Editor of the Journal of Statistical Education. He is co-author of the book Statistical Methods for Behavioral Ecology and received a Fulbright scholarship under the American Republics Research program to work at the Charles Darwin Research Station in the Galapagos Islands. Professor Fligner's research interests are in Nonparametric Statistical methods and he received the Statistics in Chemistry award from the American Statistical Association for work on detecting biologically active compounds. He has done consulting work with several large corporations in Central Ohio. He spent almost 40 years at the Ohio State University where he was Vice Chair of the Department for over 10 years and also served as Director of the Statistical Consulting Service. in mathematics from the State University of New York at Stony Brook and his Ph.D. Fligner is an Adjunct Professor at the University of California at Santa Cruz and a non-resident Professor Emeritus with the Ohio State University. Part VI: Optional Companion Chapters Available OnlineĬhapter 32 Resampling: Permutation Tests and the Bootstrap Part III: From Data Production to InferenceĬhapter 16 Confidence Intervals: The BasicsĬhapter 17 Tests of Significance: The BasicsĬhapter 19 From Data Production to Inference: Part III ReviewĬhapter 20 Inference about a Population MeanĬhapter 22 Inference about a Population ProportionĬhapter 24 Inference about Variables: Part IV ReviewĬhapter 25 Categorical Variables: The Chi-Square TestĬhapter 27 One-Way Analysis of Variance: Comparing Several Means Chapter 1 Picturing Distributions with GraphsĬhapter 2 Describing Distributions with NumbersĬhapter 11 Producing Data: Part II Review


 0 kommentar(er)
0 kommentar(er)
